08、后序遍历Morris

厨子大约 6 分钟数据结构算法基础面试题解析二叉树遍历程序厨校招社招算法题精讲

后序遍历的 Morris 方法也比之前两种代码稍微长一些，看着挺唬人,其实不难，和我们之前说的没差多少。下面我们一起来干掉它吧。

我们先来复习下之前说过的中序遍历，见下图。

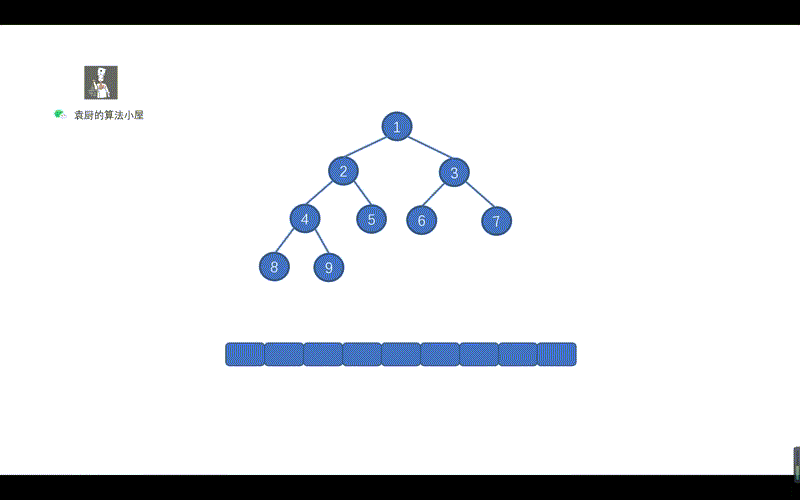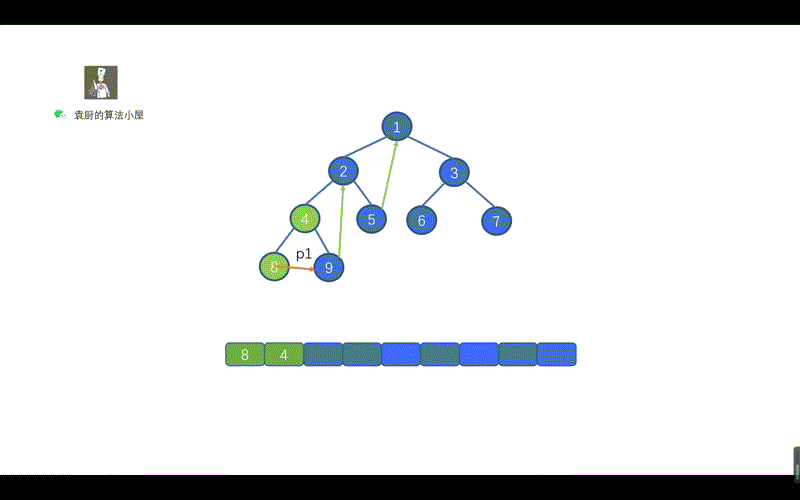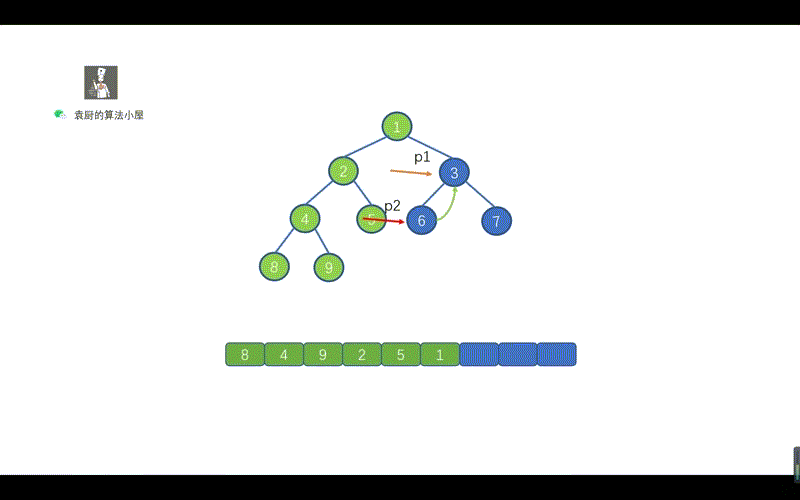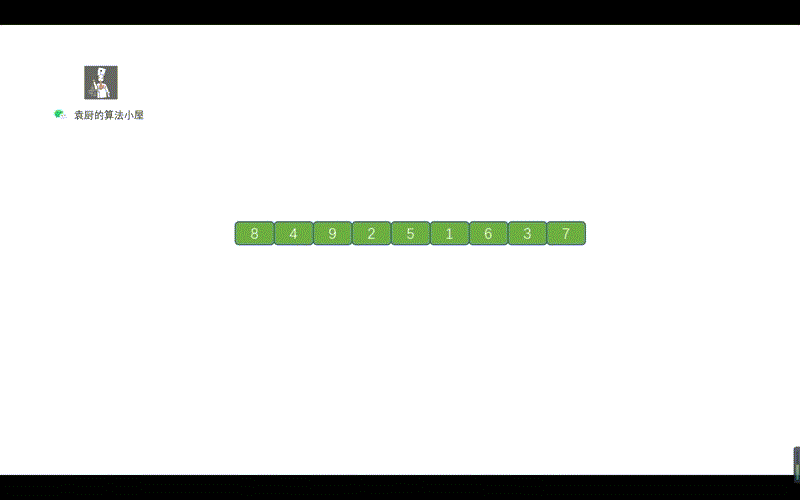
另外我们来对比下，中序遍历和后序遍历的 Morris 方法，代码有哪里不同。

由上图可知，仅仅有三处不同，后序遍历里少了 list.add()，多了一个函数postMorris() ，那后序遍历的 list.add() 肯定是在 postMorris 函数中的。所以我们搞懂了 postMorris 函数，也就搞懂了后序遍历的 Morris 方法（默认大家看了之前的文章，没有看过的同学，可以点击文首的链接）

下面我们一起来剖析下 postMorris 函数.代码如下

#include <vector>
using namespace std;

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    // 构造函数
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

class Solution {
private:
    // 存储后序遍历结果的容器
    vector<int> result;

    // 反转链表（对应原 reverseList 方法）
    TreeNode* reverseList(TreeNode* head) {
        TreeNode* cur = head;
        TreeNode* pre = nullptr;
        while (cur != nullptr) {
            TreeNode* next = cur->right;  // 注意：原逻辑是基于右指针模拟链表
            cur->right = pre;
            pre = cur;
            cur = next;
        }
        return pre;
    }

public:
    // 后序 Morris 遍历
    void postMorris(TreeNode* root) {
        // 反转右指针链表
        TreeNode* reverseNode = reverseList(root);
        // 遍历反转后的链表（原右指针方向）
        TreeNode* cur = reverseNode;
        while (cur != nullptr) {
            result.push_back(cur->val);  // 存入节点值
            cur = cur->right;
        }
        // 反转恢复原链表结构
        reverseList(reverseNode);
    }

    // 可选：提供获取结果的接口（方便外部访问遍历结果）
    vector<int> getPostOrderResult() {
        return result;
    }
};

上面的代码，是不是贼熟悉，和我们的倒序输出链表一致，步骤为，反转链表，遍历链表，将链表反转回原样。只不过我们将 ListNode.next 写成了 TreeNode.right 将树中的遍历右子节点的路线，看成了一个链表，见下图。

动画模拟

上图中的一个绿色虚线，代表一个链表，我们根据序号进行倒序遍历，看下是什么情况

到这块是不是就整懂啦，打完收工！

代码

Java

class Solution {
    List<Integer> list;
    public List<Integer> postorderTraversal(TreeNode root) {
        list = new ArrayList<>();
        if (root == null) {
            return list;
        }
        TreeNode p1 = root;
        TreeNode p2 = null;
        while (p1 != null) {
            p2 = p1.left;
            if (p2 != null) {
                 while (p2.right != null && p2.right != p1) {
                     p2 = p2.right;
                 }
                 if (p2.right == null) {
                     p2.right = p1;
                     p1 = p1.left;
                     continue;
                 } else {
                     p2.right = null;
                     postMorris(p1.left);
                 }
            }
            p1 = p1.right;
        }
        //以根节点为起点的链表
        postMorris(root);
        return list;
    }
    public void postMorris(TreeNode root) {
        //翻转链表
        TreeNode reverseNode = reverseList(root);
        //从后往前遍历
        TreeNode cur = reverseNode;
        while (cur != null) {
            list.add(cur.val);
            cur = cur.right;
        }
        //翻转回来
        reverseList(reverseNode);
    }
    public TreeNode reverseList(TreeNode head) {
        TreeNode cur = head;
        TreeNode pre = null;
        while (cur != null) {
            TreeNode next = cur.right;
            cur.right = pre;
            pre = cur;
            cur = next;
        }
        return pre;
    }

}

C++

#include <vector>

// 二叉树节点定义
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
private:
    std::vector<int> list;  // 存储遍历结果（对应Java的成员变量list）

    // 翻转以right指针连接的链表（类似单链表翻转）
    TreeNode* reverseList(TreeNode* head) {
        TreeNode* cur = head;
        TreeNode* pre = nullptr;
        while (cur != nullptr) {
            TreeNode* next = cur->right;  // 记录下一个节点（通过right指针连接）
            cur->right = pre;  // 翻转指针方向
            pre = cur;
            cur = next;
        }
        return pre;  // 返回翻转后的头节点
    }

    // 处理以root为起点的右线索链表，添加后序遍历结果
    void postMorris(TreeNode* root) {
        TreeNode* reverseNode = reverseList(root);  // 翻转链表
        TreeNode* cur = reverseNode;
        // 遍历翻转后的链表（实际是原链表的反向），收集节点值
        while (cur != nullptr) {
            list.push_back(cur->val);
            cur = cur->right;
        }
        reverseList(reverseNode);  // 再次翻转恢复原链表结构（不影响结果，保持树完整性）
    }

public:
    std::vector<int> postorderTraversal(TreeNode* root) {
        list.clear();  // 清空结果集（避免多次调用时残留数据）
        if (root == nullptr) {
            return list;
        }

        TreeNode* p1 = root;  // 主指针，遍历树的节点
        TreeNode* p2 = nullptr;  // 辅助指针，用于找左子树最右节点

        while (p1 != nullptr) {
            p2 = p1->left;  // p2指向p1的左子树
            if (p2 != nullptr) {
                // 找到左子树的最右节点，且右指针未指向p1（避免循环）
                while (p2->right != nullptr && p2->right != p1) {
                    p2 = p2->right;
                }

                // 情况1：最右节点右指针为空（首次访问左子树）
                if (p2->right == nullptr) {
                    p2->right = p1;  // 建立线索，指向p1
                    p1 = p1->left;  // 移动p1到左子树
                    continue;
                }
                // 情况2：最右节点右指针已指向p1（左子树已遍历完）
                else {
                    p2->right = nullptr;  // 撤销线索
                    postMorris(p1->left);  // 处理左子树的后序遍历
                }
            }
            // 移动p1到右子树（左子树已处理或无左子树）
            p1 = p1->right;
        }

        // 处理以根节点为起点的右线索链表（最后处理根节点相关的后序部分）
        postMorris(root);

        return list;
    }
};