05、中序遍历迭代

哈喽大家好，我是厨子，之前我们说了二叉树前序遍历的迭代法和 Morris，今天咱们写一下中序遍历的迭代法和 Morris。

中序遍历的顺序是, 对于树中的某节点,先遍历该节点的左子树, 然后再遍历该节点, 最后遍历其右子树。老规矩，上动画，我们先通过动画回忆一下二叉树的中序遍历。

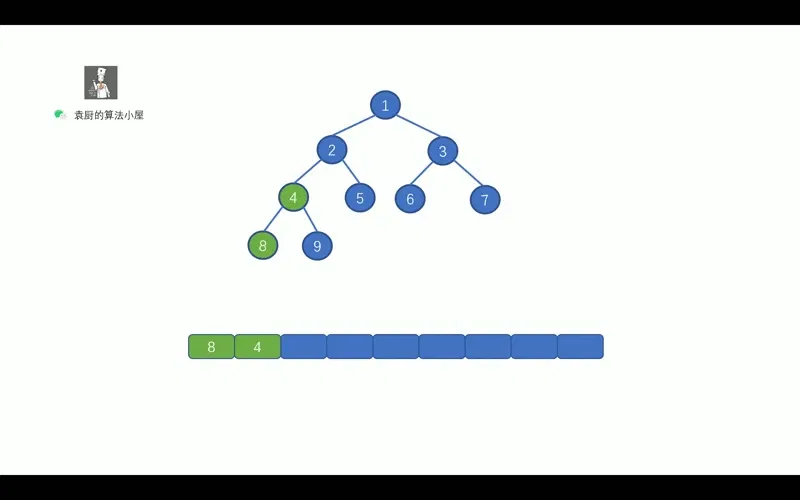
我们二叉树的中序遍历迭代法和前序遍历是一样的，都是借助栈来帮助我们完成。

我们结合动画思考一下，该如何借助栈来实现呢？

我们来看下面这个动画。

动画模拟

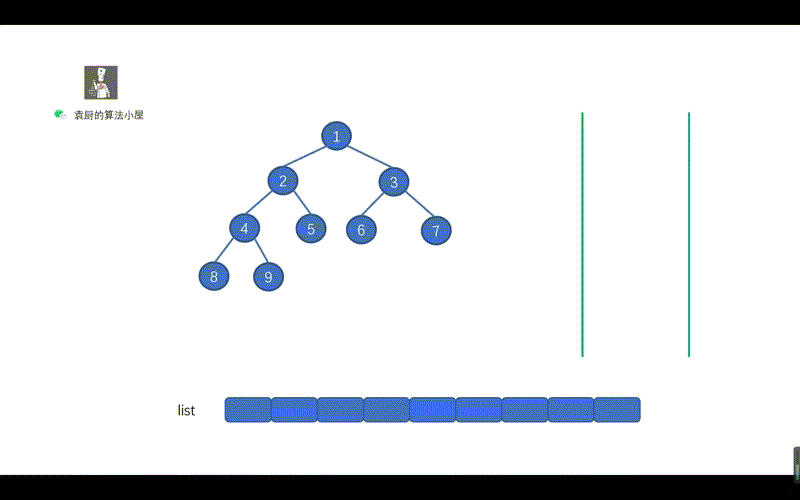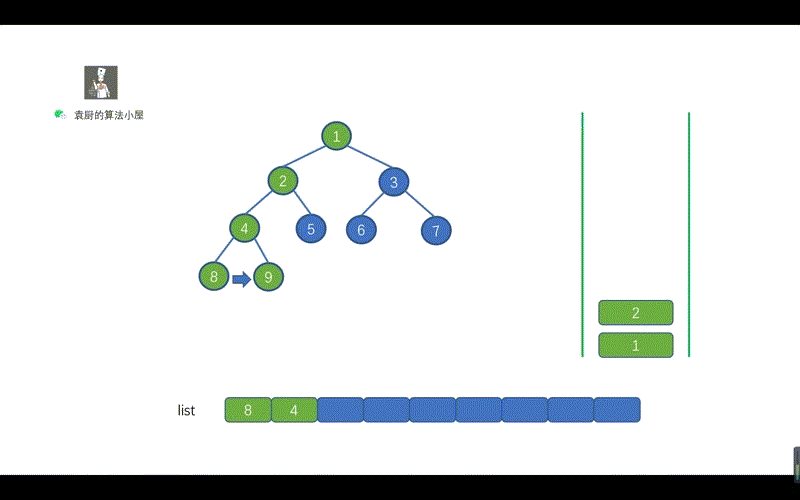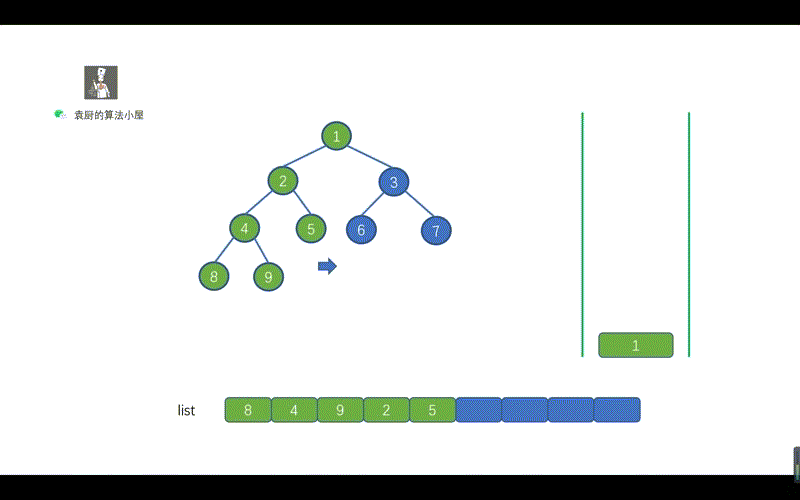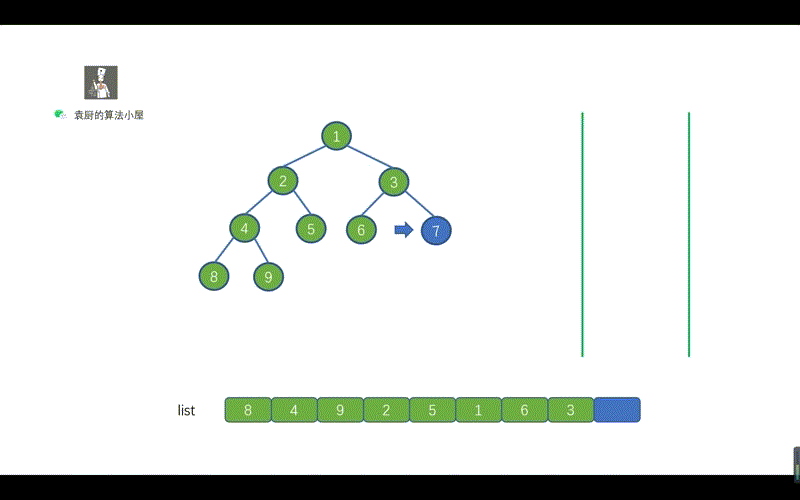
用栈实现的二叉树的中序遍历有两个关键的地方。

• 指针不断向节点的左孩子移动，为了找到我们当前需要遍历的节点。途中不断执行入栈操作
• 当指针为空时，则开始出栈，并将指针指向出栈节点的右孩子。

这两个关键点也很容易理解，指针不断向左孩子移动，是为了找到我们此时需要节点。然后当指针指向空时，则说明我们此时已经找到该节点，执行出栈操作，并将其值存入 list 即可，另外我们需要将指针指向出栈节点的右孩子，迭代执行上诉操作。

大家是不是已经知道怎么写啦，下面我们看代码吧。

代码

#include <vector>
#include <stack>

// 二叉树节点定义
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    std::vector<int> inorderTraversal(TreeNode* root) {
        std::vector<int> result;  // 存储遍历结果
        std::stack<TreeNode*> stk;  // 辅助栈
        TreeNode* cur = root;  // 当前遍历节点指针
        
        // 循环条件：栈不为空 或 当前节点不为空
        while (!stk.empty() || cur != nullptr) {
            // 1. 遍历左子树：将所有左节点入栈，直到无左子节点
            while (cur != nullptr) {
                stk.push(cur);
                cur = cur->left;
            }
            
            // 2. 弹出栈顶节点（此时左子树已遍历完），访问该节点
            TreeNode* temp = stk.top();
            stk.pop();
            result.push_back(temp->val);
            
            // 3. 转向右子树，继续上述过程
            cur = temp->right;
        }
        
        return result;
    }
};