06、中序遍历Morris

厨子大约 5 分钟数据结构算法基础面试题解析二叉树遍历程序厨校招社招算法题精讲

我们之前说过，前序遍历的 Morris 方法，如果已经掌握，今天中序遍历的 Morris 方法也就没有什么难度，仅仅修改了一丢丢。

我们先来回顾一下前序遍历 Morris 方法的代码部分。

前序遍历 Morris 代码

#include <vector>

// 二叉树节点定义
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    std::vector<int> preorderTraversal(TreeNode* root) {
        std::vector<int> result;  // 存储遍历结果
        if (root == nullptr) {    // 空树直接返回空结果
            return result;
        }
        
        TreeNode* p1 = root;  // 主指针，遍历树的节点
        TreeNode* p2 = nullptr;  // 辅助指针，用于找左子树最右节点
        
        while (p1 != nullptr) {
            p2 = p1->left;  // p2指向p1的左子树
            
            if (p2 != nullptr) {  // 若存在左子树
                // 找到左子树的最右叶子节点，且该节点的右指针未指向p1（避免循环）
                while (p2->right != nullptr && p2->right != p1) {
                    p2 = p2->right;
                }
                
                // 情况1：最右节点的右指针为空（首次访问左子树）
                if (p2->right == nullptr) {
                    result.push_back(p1->val);  // 前序：先访问根节点
                    p2->right = p1;  // 建立线索，指向p1（父节点）
                    p1 = p1->left;  // 移动p1到左子树
                    continue;  // 继续处理左子树
                } 
                // 情况2：最右节点的右指针已指向p1（左子树已遍历完）
                else {
                    p2->right = nullptr;  // 撤销线索，恢复树结构
                }
            } 
            // 若不存在左子树（直接访问当前节点）
            else {
                result.push_back(p1->val);
            }
            
            // 移动p1到右子树（左子树已处理或无左子树）
            p1 = p1->right;
        }
        
        return result;
    }
};

我们先来看标注 1 的部分，这里的含义是，当找到 p1 指向节点的左子树中的最右子节点时。也就是下图中的情况，此时我们需要将 p1 指向的节点值，存入 list。

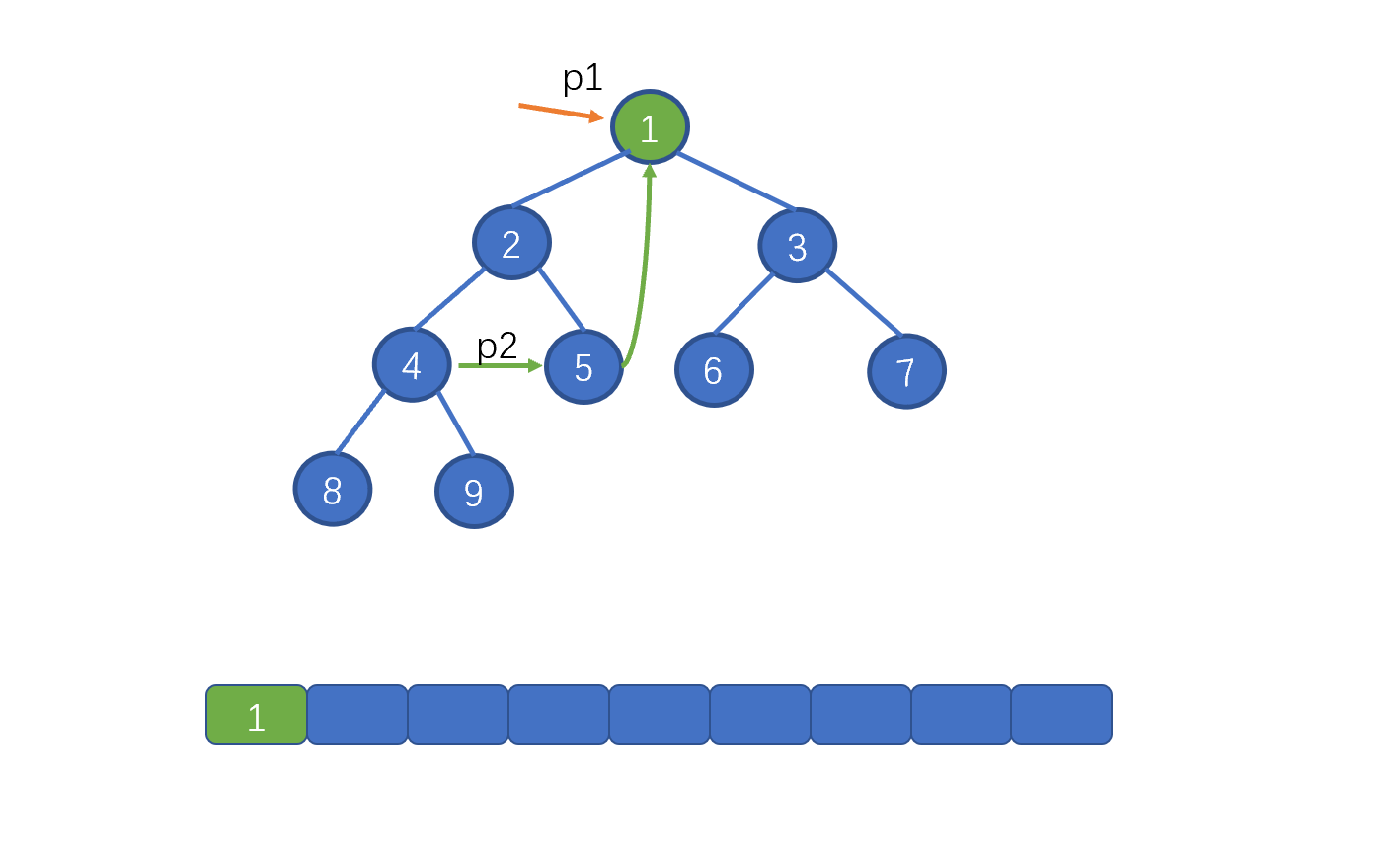
上述为前序遍历时的情况，那么中序遍历应该如何操作嘞。

前序遍历我们需要移动 p1 指针，p1 = p1.left 这样做的原因和上述迭代法原理一致，找到我们当前需要遍历的那个节点。

我们还需要修改哪里呢？见下图

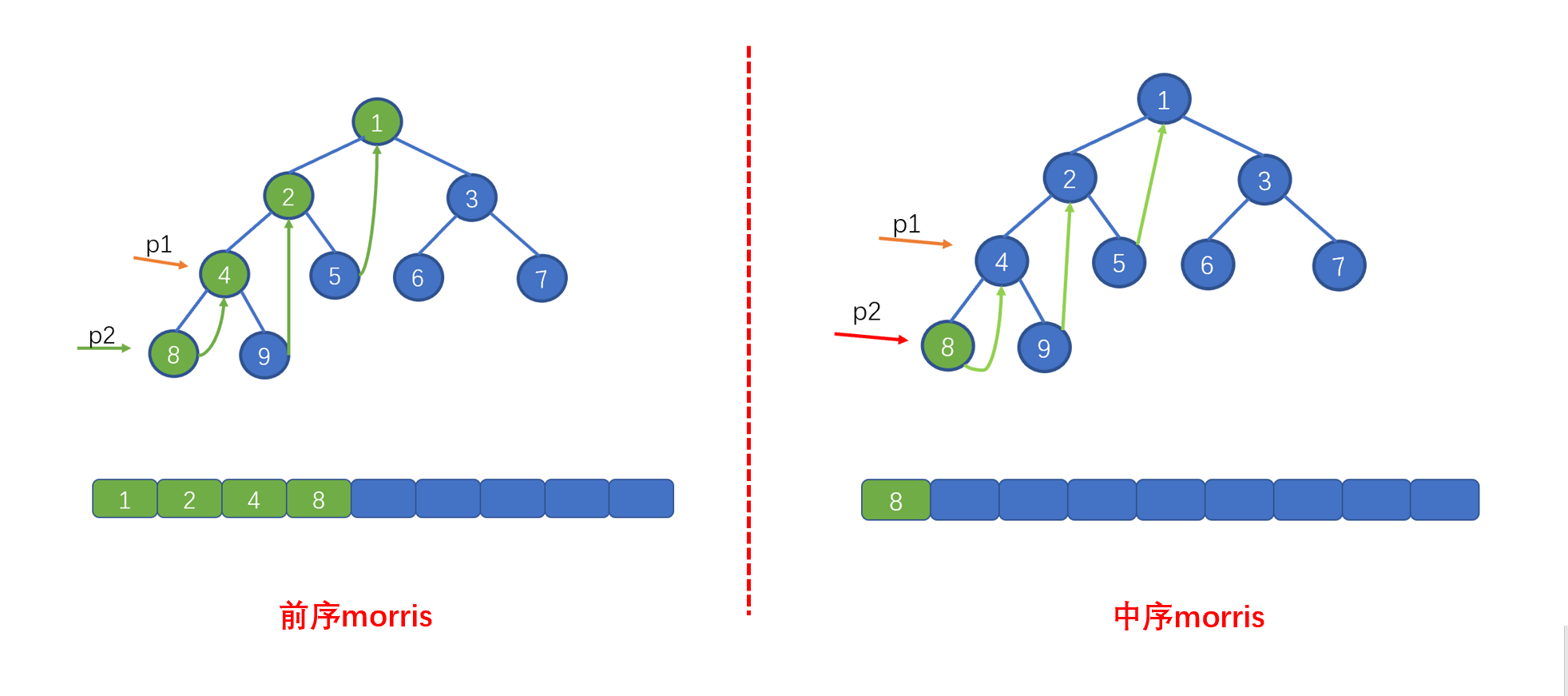
我们在前序遍历时，遇到 p2.right == p1的情况时，则会执行 p2.right == null 并让 p1 = p1.right,这样做是因为，我们此时 p1 指向的值已经遍历完毕，为了防止重复遍历。

但是呢，在我们的中序 Morris 中我们遇到p2.right == p1此时 p1 还未遍历，所以我们需要在上面两条代码之间添加一行代码list.add(p1.val);

好啦，到这里我们就基本上就搞定了中序遍历的 Morris 方法，下面我们通过动画来加深一下印象吧，当然我也会把前序遍历的动画放在这里，大家可以看一下哪里有所不同。

动画模拟

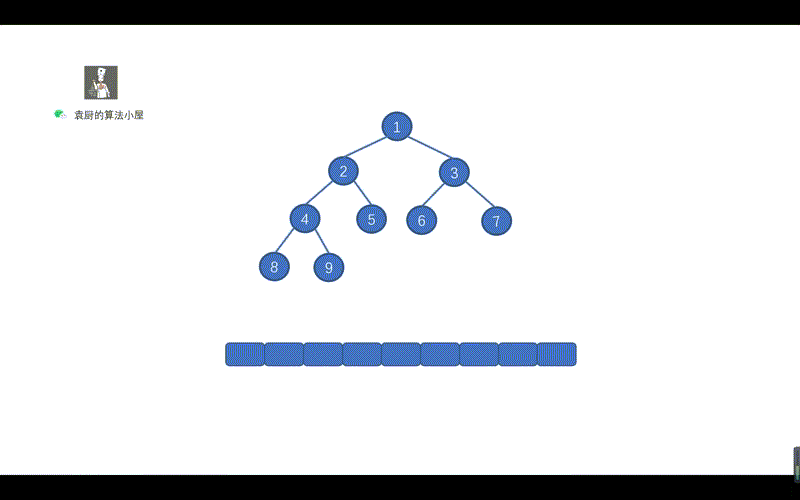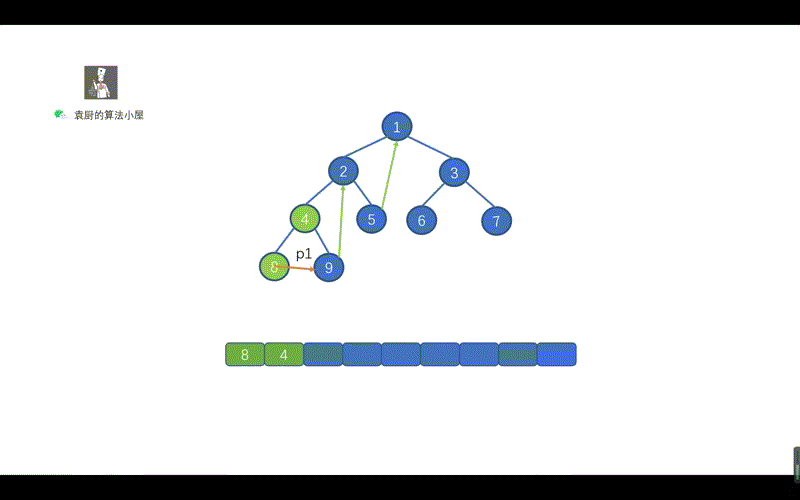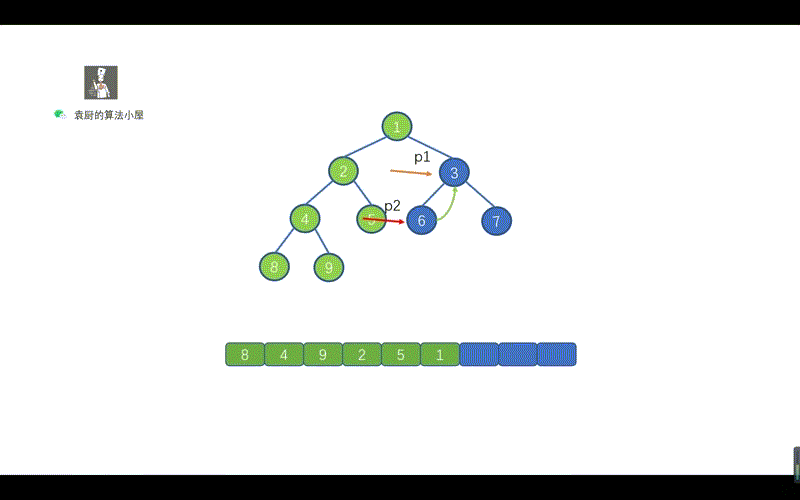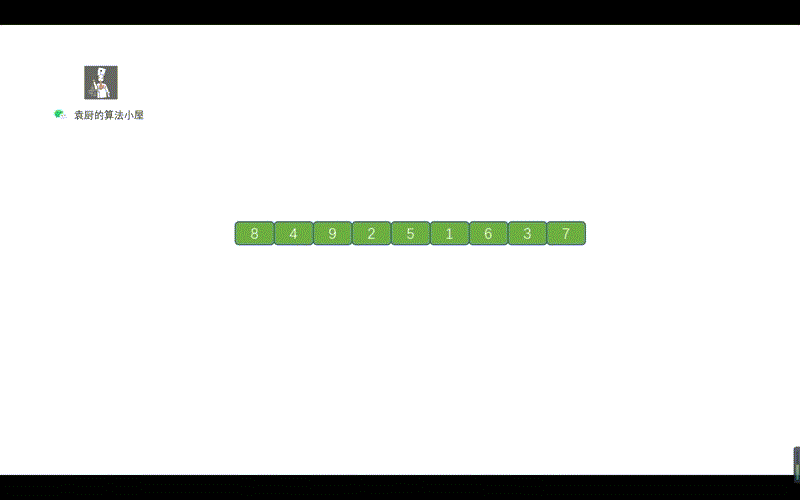
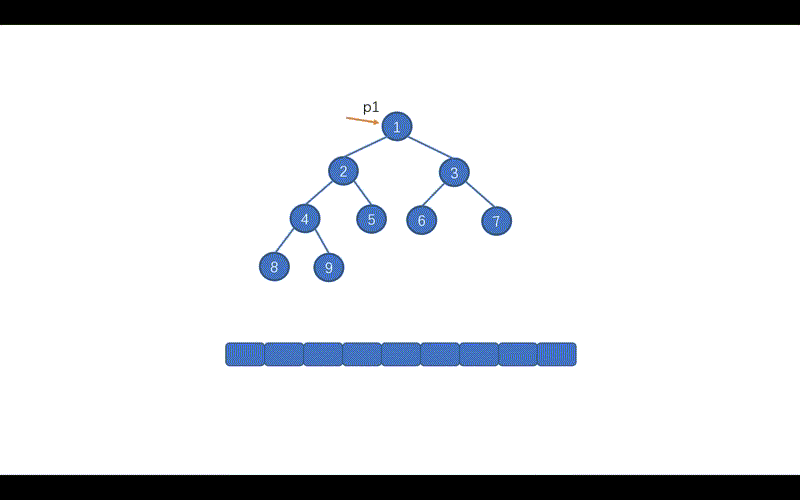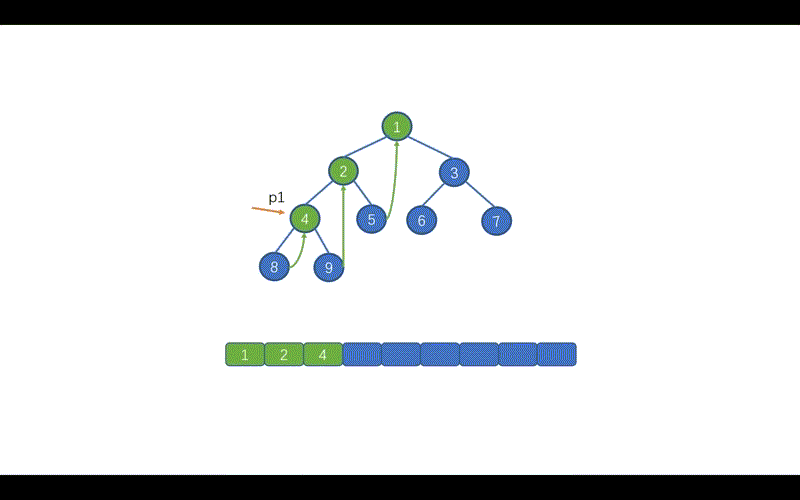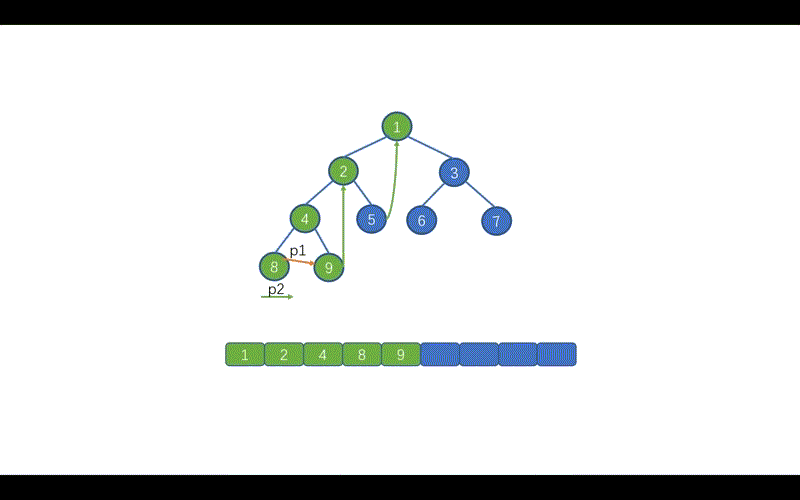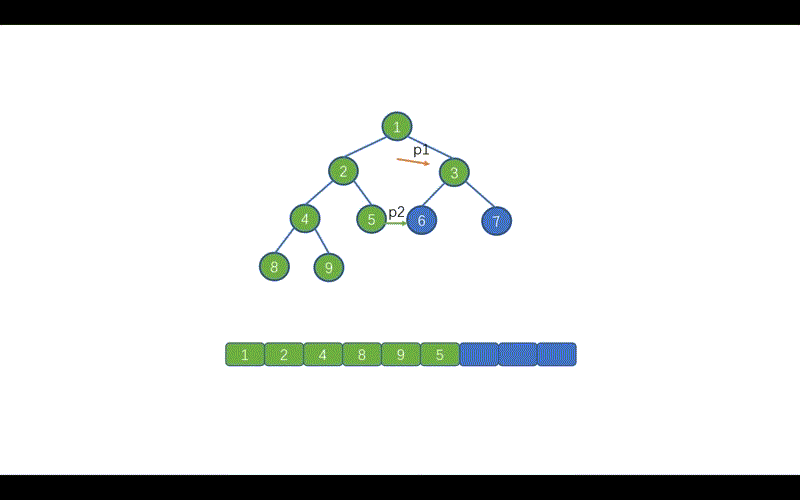
代码

#include <vector>

// 二叉树节点定义
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    std::vector<int> inorderTraversal(TreeNode* root) {
        std::vector<int> result;  // 存储遍历结果
        if (root == nullptr) {    // 空树直接返回空结果
            return result;
        }
        
        TreeNode* p1 = root;  // 主指针，遍历树的节点
        TreeNode* p2 = nullptr;  // 辅助指针，用于找左子树最右节点
        
        while (p1 != nullptr) {
            p2 = p1->left;  // p2指向p1的左子树
            
            if (p2 != nullptr) {  // 若存在左子树
                // 找到左子树的最右节点，且该节点的右指针未指向p1（避免循环）
                while (p2->right != nullptr && p2->right != p1) {
                    p2 = p2->right;
                }
                
                // 情况1：最右节点的右指针为空（首次访问左子树）
                if (p2->right == nullptr) {
                    p2->right = p1;  // 建立线索，指向p1（父节点）
                    p1 = p1->left;  // 移动p1到左子树
                    continue;  // 继续处理左子树
                } 
                // 情况2：最右节点的右指针已指向p1（左子树已遍历完）
                else {
                    p2->right = nullptr;  // 撤销线索，恢复树结构
                }
            } 
            
            // 中序遍历核心：左子树处理完后，访问当前节点（左→根→右）
            result.push_back(p1->val);
            // 移动p1到右子树（左子树已处理或无左子树）
            p1 = p1->right;
        }
        
        return result;
    }
};

06、中序遍历Morris

# 动画模拟

# 代码

动画模拟

代码