04、队列

厨子大约 19 分钟数据结构算法基础面试题解析队列程序厨校招社招

哈喽，大家好，我是厨子，今天给大家介绍一下数据结构里面的队列，希望能够对大家有一些帮助

完成这个文章的学习，你将收获

什么是队列，队列的特性，队列的基本操作，队列的实现方式，队列的变体，队列的应用场景等知识，下面我们逐一讲解

什么是队列

我们首先来看一下什么是队列？同样是引入一个现实中的列子，来帮助大家理解

生活中的队列

队列（Queue）是一种先进先出（First In First Out，FIFO）的数据结构。

大家肯定有过排队买票的经验，那先排队的先买，也就是我们说的先进先出

排队买票：

队列的定义

队列是一种线性数据结构，只允许在一端（队尾）插入，在另一端（队首）删除。

像栈一样，队列（queue）也是表。然而使用队列时插入在一端进行而删除在另一端进行，遵守先进先出的规则。所以队列的另一个名字是（FIFO）。

队列的基本操作

入队（enqueue）：它是在表的末端(队尾(rear)插入一个元素。

出队（dequeue）: 出队他是删除在表的开头（队头(front)）的元素。

注：下面模型只象征着输入输出操作

具体模型

核心特点：

先进先出（FIFO）
队尾入队（enqueue）
队首出队（dequeue）

提到队列，就离不开栈，下面我们来看一下，栈和队列的对比，在之前的文章中，也给大家讲解了，什么是栈

队列 vs 栈

特性	队列（Queue）	栈（Stack）
原则	FIFO（先进先出）	LIFO（后进先出）
插入位置	队尾	栈顶
删除位置	队首	栈顶
生活类比	排队	叠盘子
应用	任务调度、BFS	函数调用、DFS

队列的基本操作

核心操作

这里为了让大家更好的理解，所以做了一个视频来模拟队列操作

操作示例（文字版）

队列的操作演示：

初始状态：空队列
Queue: []

1. enqueue(10):
   Queue: [10]
   队首 ← [10] ← 队尾

2. enqueue(20):
   Queue: [10, 20]
   队首 ← [10][20] ← 队尾

3. enqueue(30):
   Queue: [10, 20, 30]
   队首 ← [10][20][30] ← 队尾

4. front():
   返回: 10
   Queue: [10, 20, 30]  （队列不变）

5. dequeue():
   返回: 10
   Queue: [20, 30]
   队首 ← [20][30] ← 队尾

6. enqueue(40):
   Queue: [20, 30, 40]
   队首 ← [20][30][40] ← 队尾

7. dequeue():
   返回: 20
   Queue: [30, 40]

8. back():
   返回: 40
   Queue: [30, 40]  （队列不变）

9. dequeue():
   返回: 30
   Queue: [40]

10. dequeue():
    返回: 40
    Queue: []

11. isEmpty():
    返回: true

至此我们应该理解了，队列的基本原理，那下面我们来看一下队列的实现方式

队列的实现方式

基于数组的实现（循环队列）

先说一下，基于数组的实现方式，此时我们有问题了？为什么是循环队列？

普通数组队列的问题：

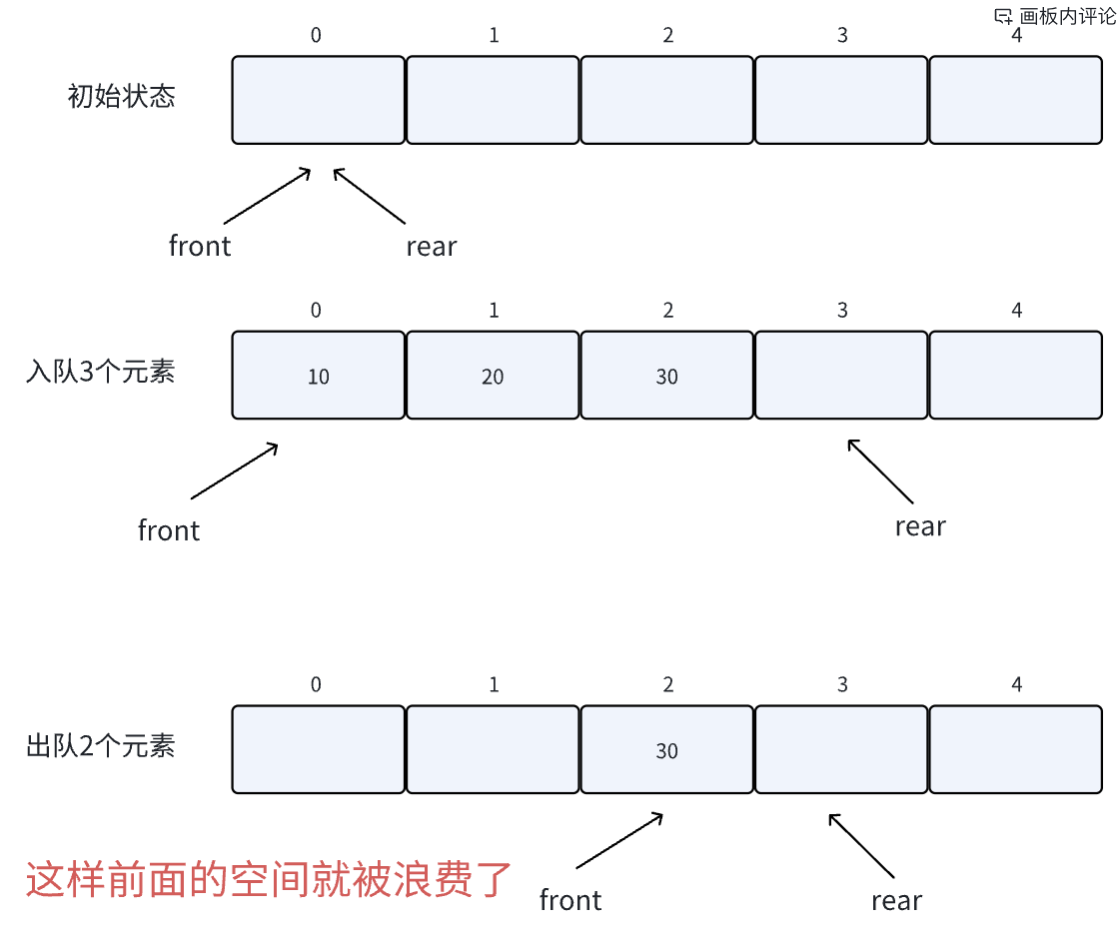
上面的队列，我们插入两个元素后想要继续插入元素，则会报溢出，虽然该数组并没有完全满，这种情况被称为假溢出

例如，我们在学校里面排队洗澡一人一个格，当你来到澡堂发现头部有两个空格，但是其余格子已经满了，你是去前面洗，还是等其他格子的哥们洗完再洗？

肯定是去前面的格子洗。除非澡堂的所有格子都满了，我们才会等。

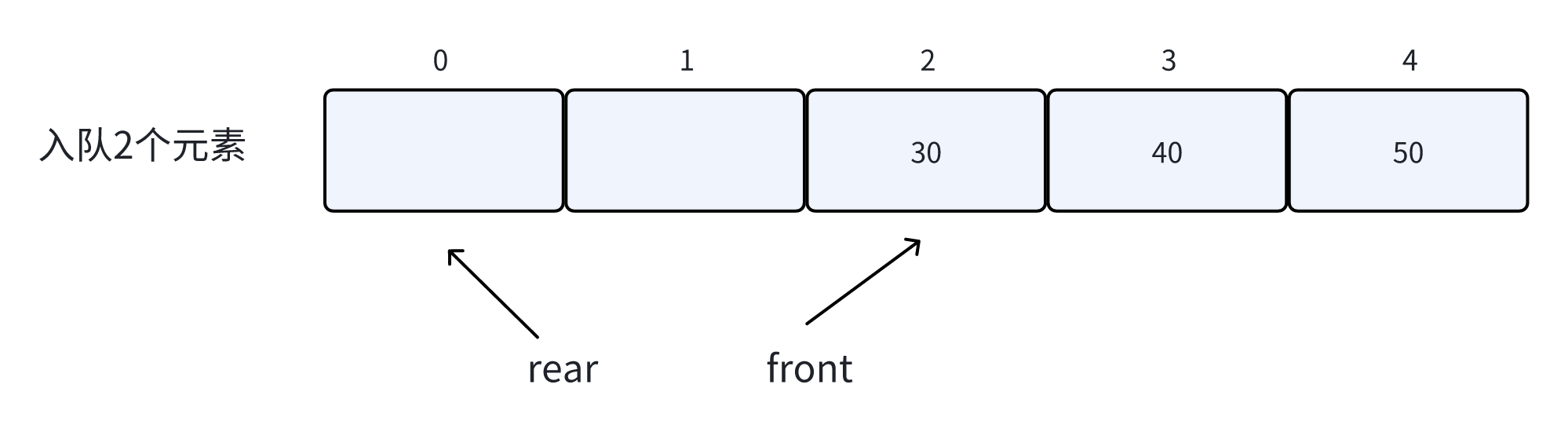
所以我们用来解决假溢出的方法就是后面满了，就再从头开始，也就是头尾相接的循环，我们把队列的这种头尾相接的顺序存储结构成为循环队列。

一句话总结，循环队列是用来解决用数组模拟队列时的假溢出问题

此时你已经知道，什么是循环队列了，那我们继续对上图，进行入队操作

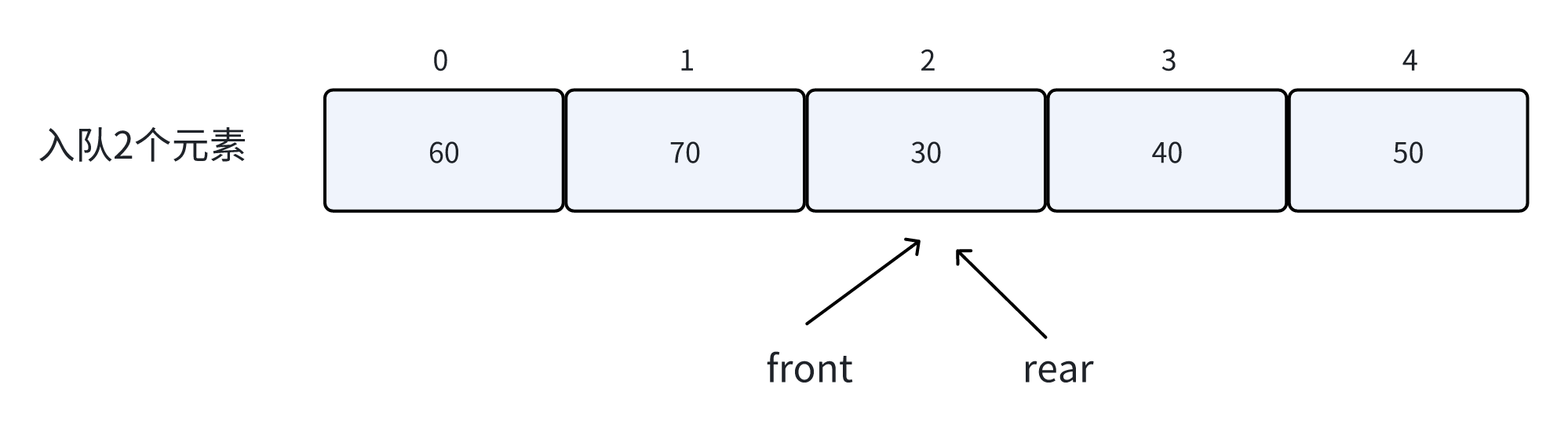
OK，我们继续插入了元素，这样所有空间都用上了，但是不知道大家，有没有发现另外一个问题？就是队列空和队列满的时均有 front == rear，那我们如何区分队列空还是满呢？

主要有两种方法

我们可以通过以下两种方法进行区分，

1.设置标记变量 flag; 当 front == rear 时且 flag = 0 时为空，当 front == rear 且 flag == 1 时为满

2.当队列为空时，front == rear, 当队列满时，我们保留一个元素空间，也就是说，队列满时，数组内还有一个空间（故意不放置内容）。

两种方式的具体介绍：

循环队列中，由于队头（front）和队尾（rear）指针会循环移动，当 front == rear 时可能表示队列空或满，需要通过特殊方式区分。常用两种两种常用方案：

标记变量法
1. 增设一个布尔型标记变量 flag（初始为 false）。
2. 空队列：front == rear 且 flag == false（初始状态或所有元素出队后）。
3. 满队列：front == rear 且 flag == true（当元素入队导致队尾追上队头时，将 flag 置为 true）。
4. 入队时，若操作后 front == rear，则 flag = true；出队时，若操作后 front == rear，则 flag = false。
5. 优点：队列空间可完全利用（数组大小为 n 时，最多存储 n 个元素）。
6. 缺点：需额外维护标记变量，逻辑稍复杂。
预留空间法
1. 不设标记，而是通过预留一个空元素空间区分状态。
2. 空队列：front == rear（初始状态或所有元素出队后）。
3. 满队列：(rear + 1) % maxSize == front（队尾指针的下一个位置是队头时，视为满）。
4. 此时队列最大存储量为 maxSize - 1（maxSize 为数组长度），始终保留一个空闲位置。
5. 优点：无需额外变量，逻辑简单，实现方便。
6. 缺点：浪费一个存储空间，当队列容量较小时，空间利用率略低。

两种方法各有侧重：标记变量法适合对空间利用率要求高的场景，预留空间法则更简洁直观，是实际开发中更常用的方案，下面则为预留空间法的实际示例

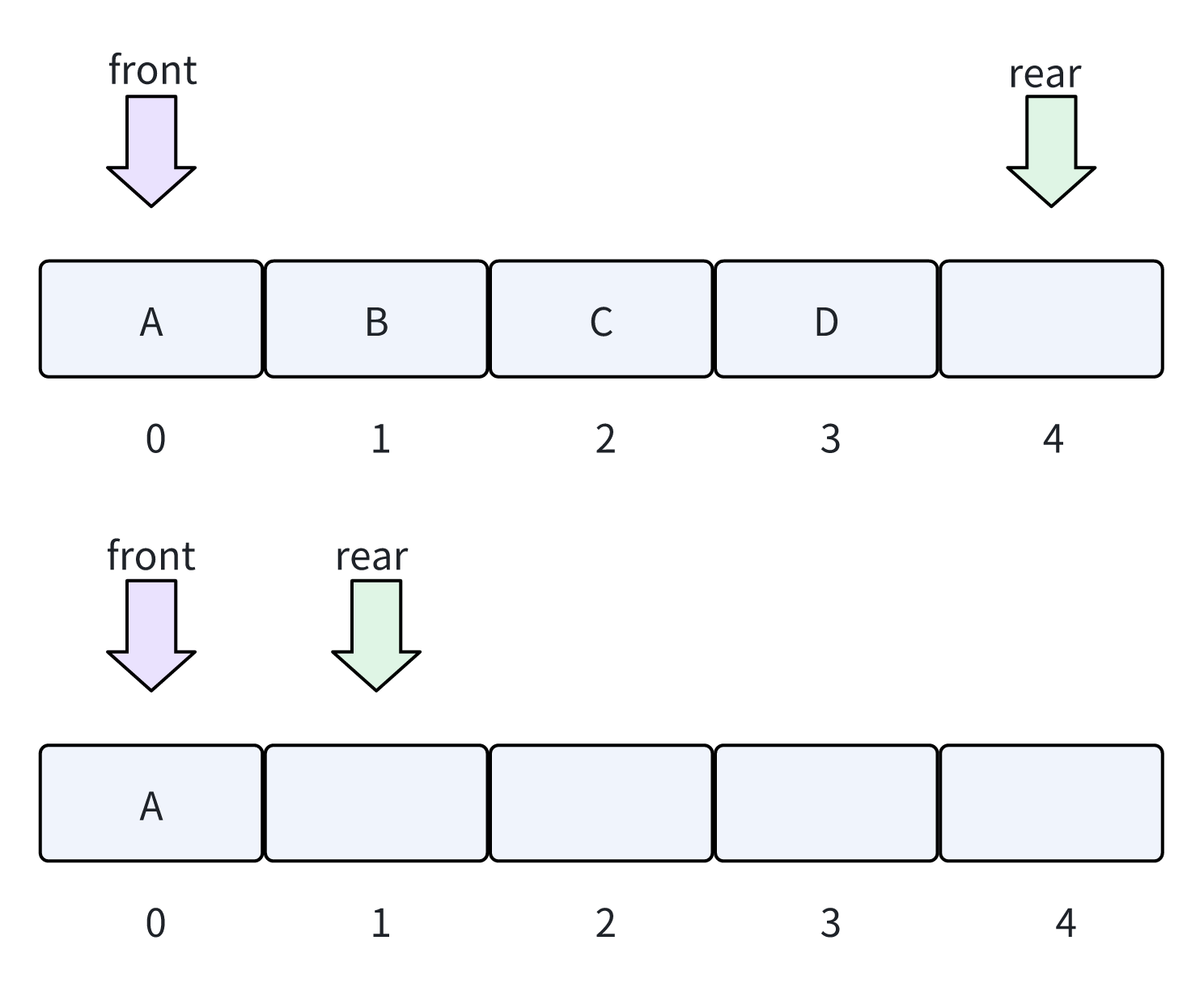
下面的代码为使用数组实现循环队列的简单 demo ，大家可以参考一下

#include <iostream>
#include <stdexcept>
using namespace std;

template <typename T>
class CircularQueue {
private:
    T* data;
    int capacity;
    int frontIndex;
    int rearIndex;
    int count;

public:
    // 构造函数
    CircularQueue(int cap = 10) : capacity(cap + 1), frontIndex(0), rearIndex(0), count(0) {
        data = new T[capacity];
        // 注意：实际可用容量是 cap，多分配一个空间用于区分满和空
    }

    // 析构函数
    ~CircularQueue() {
        delete[] data;
    }

    // 入队
    void enqueue(const T& value) {
        if (isFull()) {
            throw runtime_error("队列已满");
        }
        data[rearIndex] = value;
        rearIndex = (rearIndex + 1) % capacity;
        count++;
    }

    // 出队
    T dequeue() {
        if (isEmpty()) {
            throw runtime_error("队列为空，无法出队");
        }
        T value = data[frontIndex];
        frontIndex = (frontIndex + 1) % capacity;
        count--;
        return value;
    }

    // 查看队首元素
    T front() const {
        if (isEmpty()) {
            throw runtime_error("队列为空");
        }
        return data[frontIndex];
    }

    // 查看队尾元素
    T back() const {
        if (isEmpty()) {
            throw runtime_error("队列为空");
        }
        int lastIndex = (rearIndex - 1 + capacity) % capacity;
        return data[lastIndex];
    }

    // 判断是否为空
    bool isEmpty() const {
        return count == 0;
    }

    // 判断是否已满
    bool isFull() const {
        return count == capacity - 1;
    }

    // 获取大小
    int size() const {
        return count;
    }

    // 打印队列内容
    void print() const {
        cout << "Queue (front -> rear): ";
        if (isEmpty()) {
            cout << "empty" << endl;
            return;
        }

        int index = frontIndex;
        for (int i = 0; i < count; i++) {
            cout << data[index] << " ";
            index = (index + 1) % capacity;
        }
        cout << endl;
    }
};

到此，使用数组实现循环队列的所有内容已经讲解完毕，下面我们来看一下该小节的关键点

循环队列的关键点

1. 判断队列满的条件：

// 牺牲一个空间
bool isFull() {
    return (rearIndex + 1) % capacity == frontIndex;
}

// 使用 count 变量（推荐）
bool isFull() {
    return count == capacity - 1;
}

2. 判断队列空的条件：

bool isEmpty() {
    return frontIndex == rearIndex;  // 或 count == 0
}

3. 循环索引计算：

index = (index + 1) % capacity;  // 向后移动
index = (index - 1 + capacity) % capacity;  // 向前移动

基于链表的实现（重点）

先来说下，使用链表实现队列的优势

动态大小: 不需要预先指定队列的最大容量，可以根据需要动态增长
高效的入队出队: 在链表的头部和尾部进行插入删除操作都是 O(1) 时间复杂度
内存利用: 不会浪费预分配的空间，按需分配内存
无溢出风险: 不会出现数组实现中的队列满的情况（除非系统内存耗尽）

链表的每个节点包含两部分：

数据域: 存储元素的值

指针域: 指向下一个节点的引用

struct Node {
    int value;      // 数据域
    Node* next;     // 指针域

    Node(int val) : value(val), next(nullptr) {}
};

链表队列需要维护两个关键指针：

front（队首指针）: 指向队列的第一个节点，用于出队操作

rear（队尾指针）: 指向队列的最后一个节点，用于入队操作

size（大小）: 记录队列中元素的个数

因为该章节为重点内容，我们来详细说一下各个操作

核心操作实现

入队操作

将新元素添加到队列末尾：

步骤：

创建新节点
如果队列为空，front 和 rear 都指向新节点
如果队列不为空，将新节点连接到 rear 之后，更新 rear 指针
增加 size

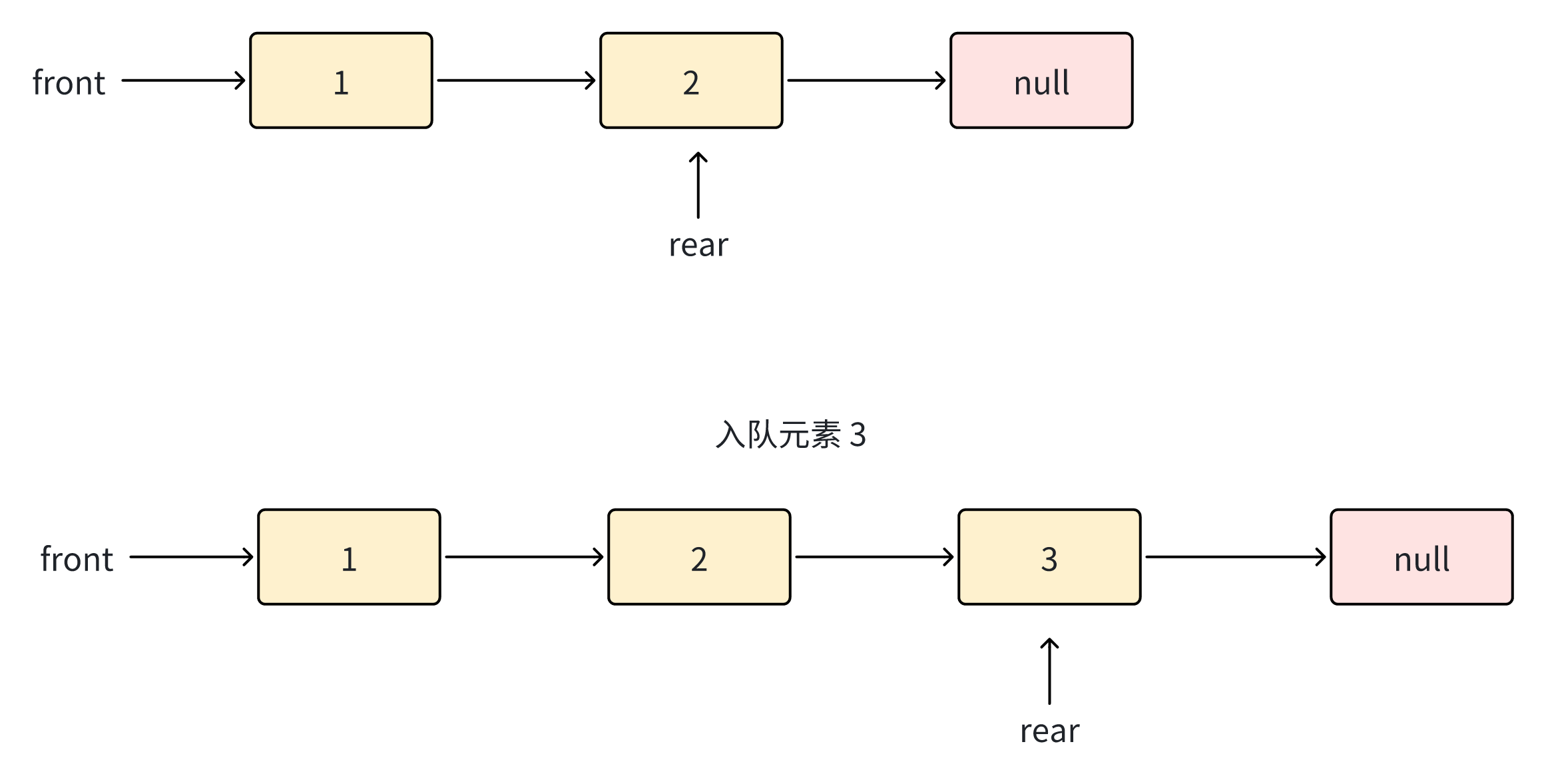
代码实现：

void enqueue(int value) {
    Node* newNode = new Node(value);

    if (isEmpty()) {
        // 队列为空，front 和 rear 都指向新节点
        front = newNode;
        rear = newNode;
    } else {
        // 队列不为空，在队尾添加新节点
        rear->next = newNode;
        rear = newNode;
    }

    size++;
}

出队操作

从队列头部移除元素：

步骤：

检查队列是否为空
保存队首节点的值
将 front 指针移动到下一个节点
如果队列变为空，将 rear 也设为 null
减少 size
返回保存的值

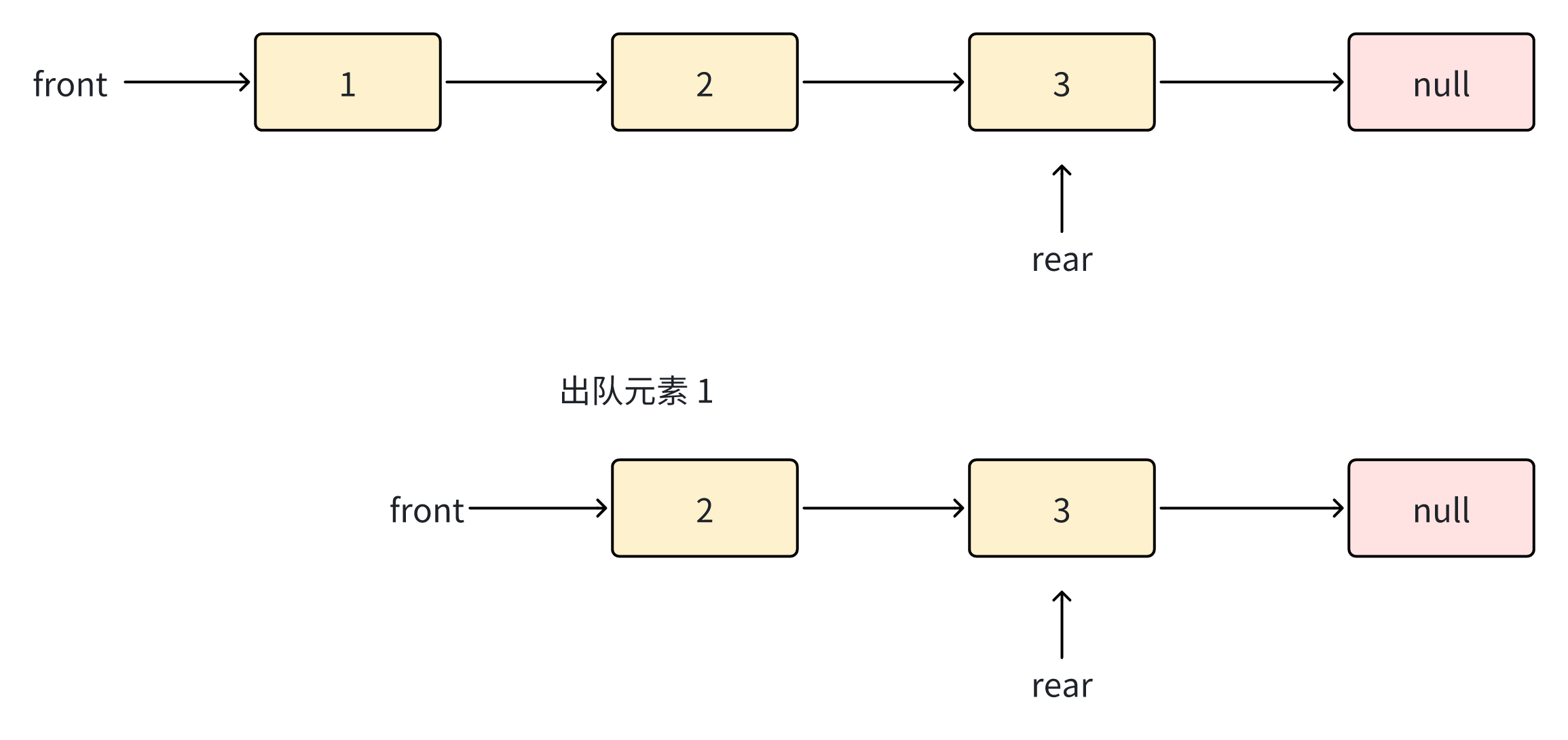
代码实现：

int dequeue() {
    if (isEmpty()) {
        throw runtime_error("队列为空，无法出队");
    }

    int value = front->value;
    Node* temp = front;
    front = front->next;

    // 如果队列变为空，rear 也要设为 nullptr
    if (front == nullptr) {
        rear = nullptr;
    }

    delete temp;  // 释放内存
    size--;
    return value;
}

查看队首

返回队首元素但不移除：

int peek() {
    if (isEmpty()) {
        throw runtime_error("队列为空");
    }
    return front->value;
}

判空

bool isEmpty() {
    return front == nullptr;
    // 或者: return size == 0;
}

获取大小

int getSize() {
    return size;
}

时间复杂度分析

操作	时间复杂度	说明
enqueue	O(1)	直接在队尾添加节点
dequeue	O(1)	直接移除队首节点
peek	O(1)	直接访问队首节点
isEmpty	O(1)	检查指针是否为空
getSize	O(1)	直接返回 size 变量

空间复杂度: O(n)，其中 n 是队列中的元素个数

到这里大家应该完全掌握了，如何使用链表来实现队列，下面来看一下完整代码吧

完整代码实现

#include <iostream>
#include <stdexcept>
#include <vector>
using namespace std;

// 节点结构
struct Node {
    int value;      // 数据域
    Node* next;     // 指针域

    Node(int val) : value(val), next(nullptr) {}
};

// 链表队列类
class LinkedListQueue {
private:
    Node* front;    // 队首指针
    Node* rear;     // 队尾指针
    int size;       // 队列大小

public:
    LinkedListQueue() : front(nullptr), rear(nullptr), size(0) {}
    ~LinkedListQueue() {
        clear();
    }
    void enqueue(int value) {
        Node* newNode = new Node(value);

        if (isEmpty()) {
            front = newNode;
            rear = newNode;
        } else {
            rear->next = newNode;
            rear = newNode;
        }

        size++;
    }

    int dequeue() {
        if (isEmpty()) {
            throw runtime_error("队列为空，无法出队");
        }

        int value = front->value;
        Node* temp = front;
        front = front->next;

        if (front == nullptr) {
            rear = nullptr;
        }

        delete temp;
        size--;
        return value;
    }

    int peek() {
        if (isEmpty()) {
            throw runtime_error("队列为空");
        }
        return front->value;
    }

    bool isEmpty() {
        return front == nullptr;
    }
   
    int getSize() {
        return size;
    }

    void clear() {
        while (!isEmpty()) {
            dequeue();
        }
    }

    vector<int> toArray() {
        vector<int> result;
        Node* current = front;

        while (current != nullptr) {
            result.push_back(current->value);
            current = current->next;
        }

        return result;
    }
    void print() {
        if (isEmpty()) {
            cout << "队列为空" << endl;
            return;
        }

        cout << "队列内容: ";
        vector<int> arr = toArray();
        for (size_t i = 0; i < arr.size(); i++) {
            cout << arr[i];
            if (i < arr.size() - 1) {
                cout << " <- ";
            }
        }
        cout << endl;
        cout << "队首: " << peek() << ", 大小: " << size << endl;
    }
};

int main() {
    // 创建队列
    LinkedListQueue queue;

    // 入队操作
    queue.enqueue(1);
    queue.enqueue(2);
    queue.enqueue(3);
    queue.enqueue(4);
    queue.print();

    // 查看队首
    cout << "队首元素: " << queue.peek() << endl;  // 输出: 1

    // 出队操作
    cout << "出队: " << queue.dequeue() << endl;   // 输出: 1
    cout << "出队: " << queue.dequeue() << endl;   // 输出: 2
    queue.print();

    // 继续入队
    queue.enqueue(5);
    queue.enqueue(6);
    queue.print();
 
    // 获取队列大小
    cout << "队列大小: " << queue.getSize() << endl;  // 输出: 4

    // 检查是否为空
    cout << "队列是否为空: " << (queue.isEmpty() ? "是" : "否") << endl;  // 输出: 否

    // 清空队列
    queue.clear();
    cout << "清空后是否为空: " << (queue.isEmpty() ? "是" : "否") << endl;  // 输出: 是

    return 0;
}

与数组实现的对比

特性	链表实现	循环数组实现
容量	动态，无上限	固定或需要扩容
入队	O(1)	O(1)，满时需 O(n) 扩容
出队	O(1)	O(1)
空间效率	需要额外指针空间	更紧凑
缓存友好性	较差	较好
随机访问	不支持	支持 O(1)

下面我们继续来看一下，队列的变体

队列的变体

这块 STL 内都有现成的，大家直接用就行，这里简单了解就好

双端队列（Deque）

双端队列（Double-Ended Queue）允许在两端进行插入和删除。

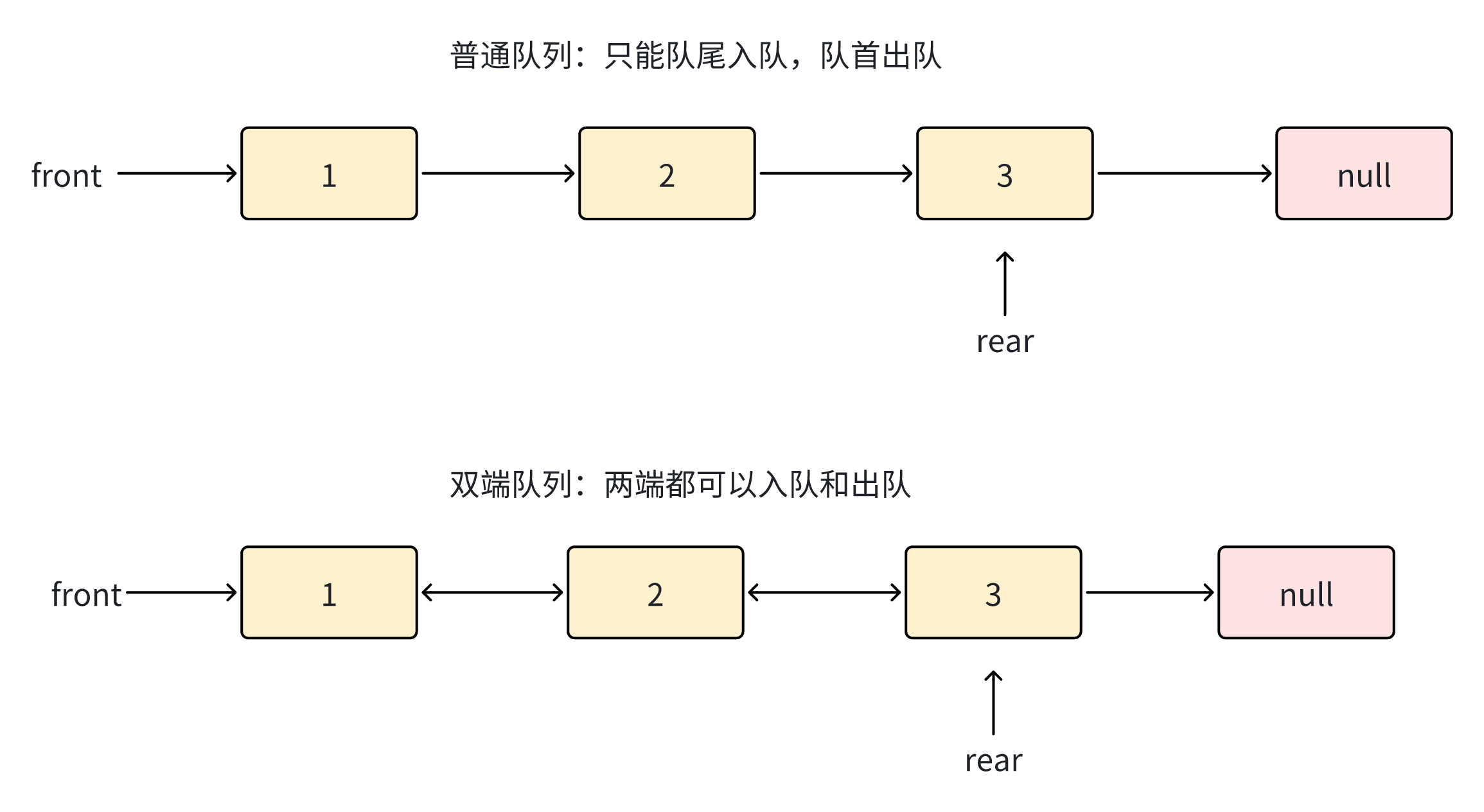
此时我们我们有疑问，为什么使用双向链表实现双端队列？

双向链表的每个节点都有前驱指针（prev）和后继指针（next），可以高效地在两端进行操作。
在双向链表的头部和尾部进行插入、删除操作都是 O(1) 时间复杂度。
可以从任意一端添加或移除元素，非常适合双端队列的需求。
不需要预先分配空间，可以根据需要动态增长。

双向节点结构

双向链表的每个节点包含三部分：

数据域（value）: 存储元素的值

前驱指针（prev）: 指向前一个节点

后继指针（next）: 指向下一个节点

struct DoubleNode {
    int value;           // 数据域
    DoubleNode* prev;    // 前驱指针
    DoubleNode* next;    // 后继指针

    // 构造函数
    DoubleNode(int val) : value(val), prev(nullptr), next(nullptr) {}
};

双端队列结构

双端队列需要维护三个关键属性：

front（队首指针）: 指向队列的第一个节点

rear（队尾指针）: 指向队列的最后一个节点

size（大小）: 记录队列中元素的个数

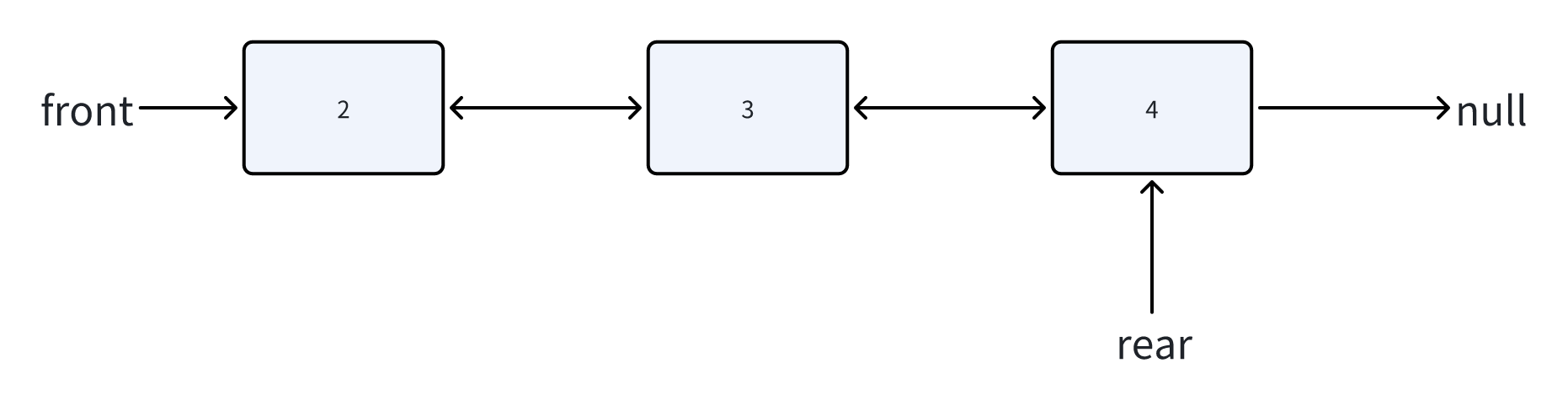
核心操作实现

队首入队

在队列头部添加新元素 1

步骤：

创建新节点
如果队列为空，front 和 rear 都指向新节点
如果队列不为空：
1. 新节点的 next 指向当前 front
2. 当前 front 的 prev 指向新节点
3. 更新 front 指针为新节点
增加 size

图解：

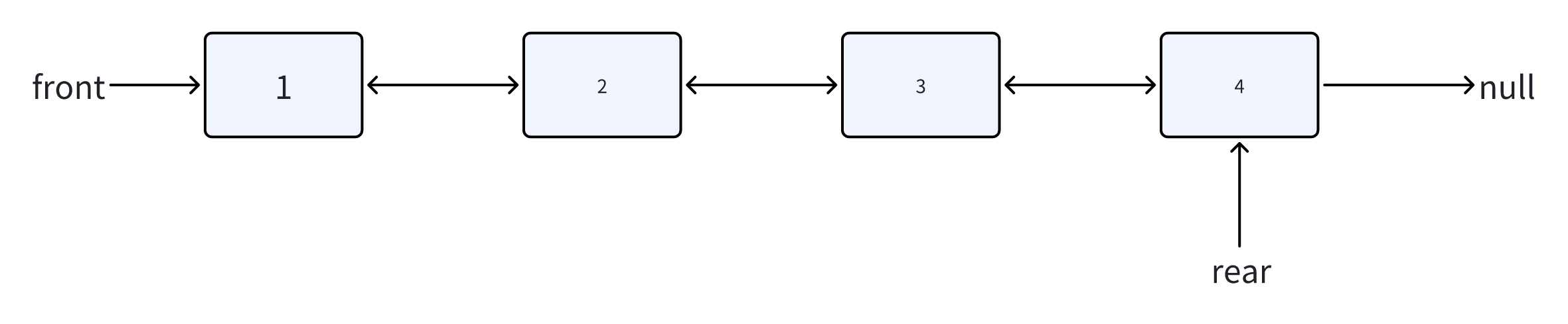
代码实现：

void enqueueFront(int value) {
    DoubleNode* newNode = new DoubleNode(value);

    if (isEmpty()) {
        // 队列为空，front 和 rear 都指向新节点
        front = newNode;
        rear = newNode;
    } else {
        // 队列不为空，在队首添加新节点
        newNode->next = front;
        front->prev = newNode;
        front = newNode;
    }

    size++;
}

队尾入队

在队列尾部添加新元素。

步骤：

创建新节点
如果队列为空，front 和 rear 都指向新节点
如果队列不为空：
1. 新节点的 prev 指向当前 rear
2. 当前 rear 的 next 指向新节点
3. 更新 rear 指针为新节点
增加 size

图解：

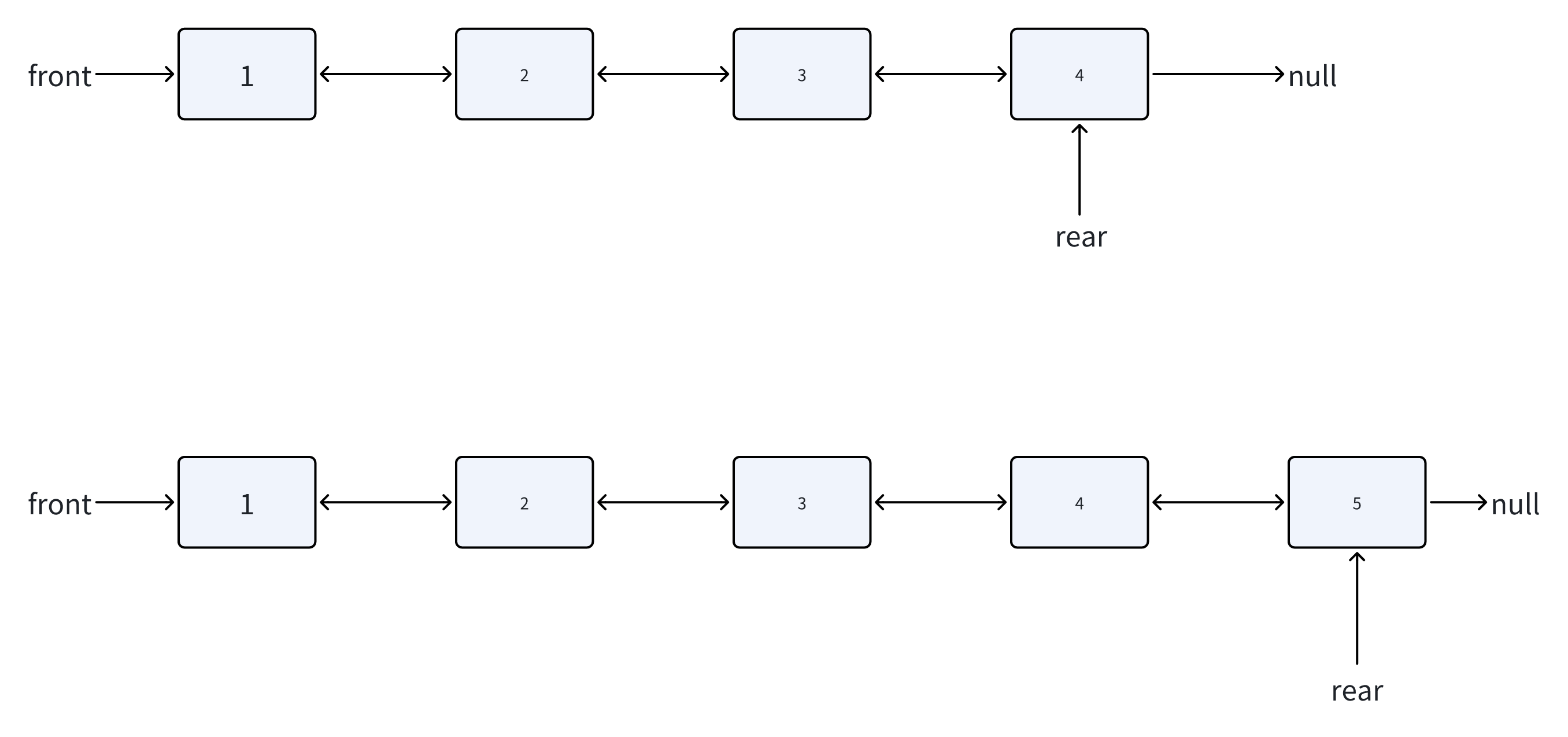
代码实现：

void enqueueRear(int value) {
    DoubleNode* newNode = new DoubleNode(value);

    if (isEmpty()) {
        // 队列为空，front 和 rear 都指向新节点
        front = newNode;
        rear = newNode;
    } else {
        // 队列不为空，在队尾添加新节点
        newNode->prev = rear;
        rear->next = newNode;
        rear = newNode;
    }

    size++;
}

队首出队

从队列头部移除元素。

步骤：

检查队列是否为空
保存队首节点的值
保存要删除的节点指针
将 front 指针移动到下一个节点
如果队列变为空，将 rear 也设为 nullptr
如果队列不为空，将新 front 的 prev 设为 nullptr
释放旧节点内存
减少 size
返回保存的值

图解：

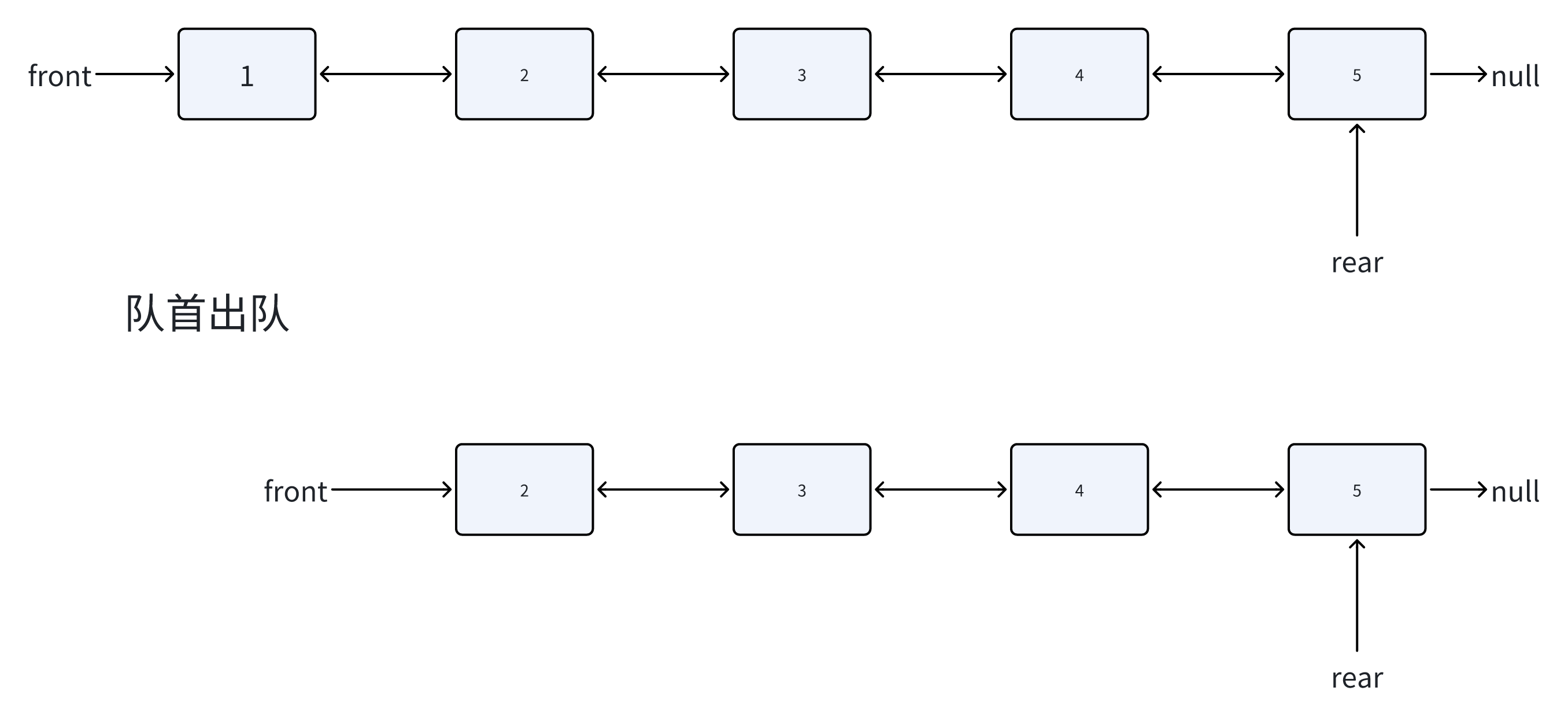
代码实现：

int dequeueFront() {
    if (isEmpty()) {
        throw runtime_error("队列为空，无法从队首出队");
    }

    int value = front->value;
    DoubleNode* temp = front;
    front = front->next;

    if (front == nullptr) {
        // 队列变为空
        rear = nullptr;
    } else {
        // 新队首的 prev 设为 nullptr
        front->prev = nullptr;
    }

    delete temp;  // 释放内存
    size--;
    return value;
}

队尾出队

从队列尾部移除元素。

步骤：

检查队列是否为空
保存队尾节点的值
保存要删除的节点指针
将 rear 指针移动到前一个节点
如果队列变为空，将 front 也设为 nullptr
如果队列不为空，将新 rear 的 next 设为 nullptr
释放旧节点内存
减少 size
返回保存的值

图解：

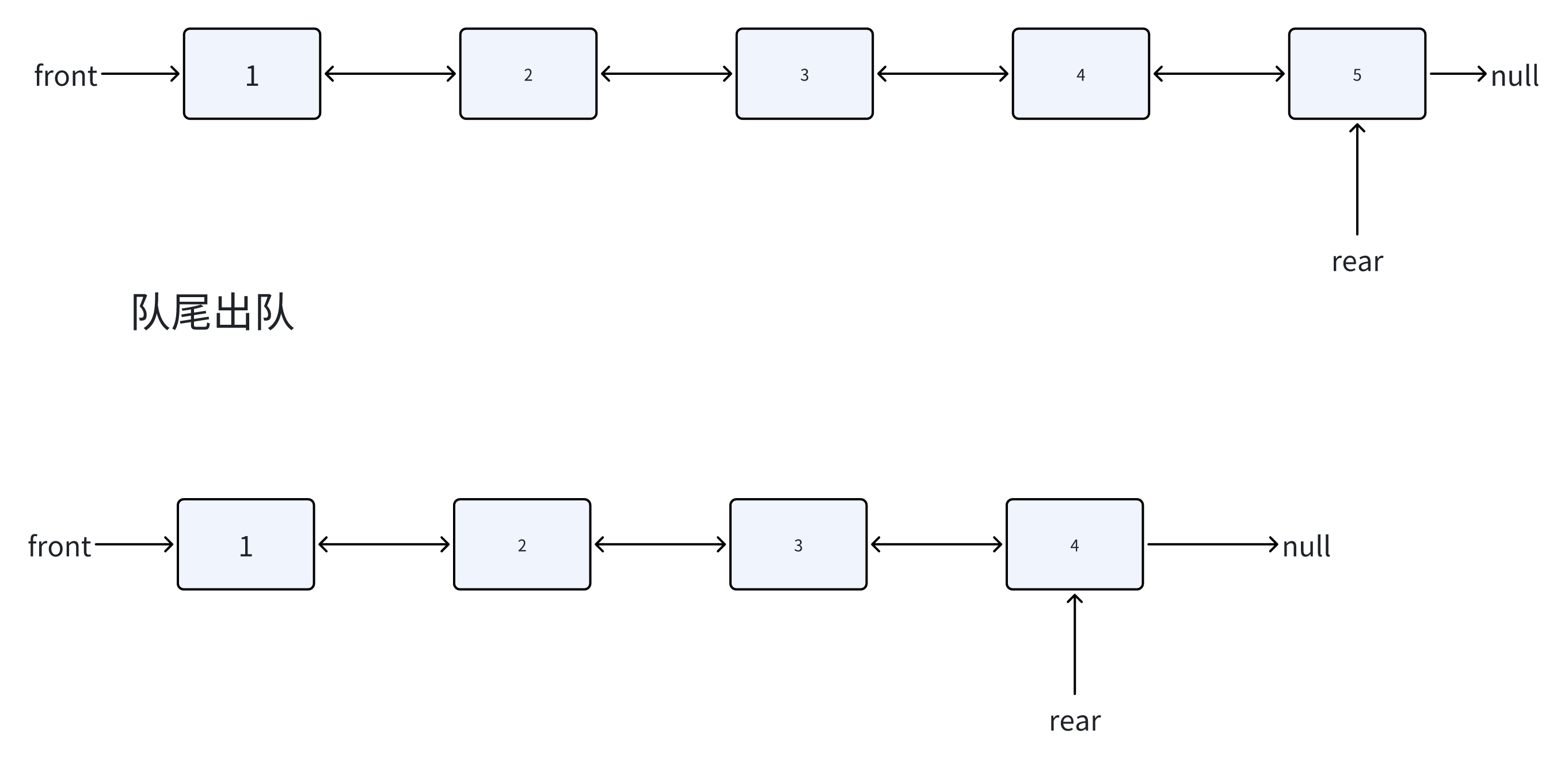
代码实现：

int dequeueRear() {
    if (isEmpty()) {
        throw runtime_error("队列为空，无法从队尾出队");
    }

    int value = rear->value;
    DoubleNode* temp = rear;
    rear = rear->prev;

    if (rear == nullptr) {
        // 队列变为空
        front = nullptr;
    } else {
        // 新队尾的 next 设为 nullptr
        rear->next = nullptr;
    }

    delete temp;  // 释放内存
    size--;
    return value;
}

查看队首和队尾

int peekFront() {
    if (isEmpty()) {
        throw runtime_error("队列为空");
    }
    return front->value;
}

int peekRear() {
    if (isEmpty()) {
        throw runtime_error("队列为空");
    }
    return rear->value;
}

判空和获取大小

bool isEmpty() {
    return front == nullptr;
    // 或者: return size == 0;
}

int getSize() {
    return size;
}

时间复杂度分析

操作	时间复杂度	说明
enqueueFront	O(1)	直接在队首添加节点
enqueueRear	O(1)	直接在队尾添加节点
dequeueFront	O(1)	直接移除队首节点
dequeueRear	O(1)	直接移除队尾节点
peekFront	O(1)	直接访问队首节点
peekRear	O(1)	直接访问队尾节点
isEmpty	O(1)	检查指针是否为空
getSize	O(1)	直接返回 size 变量

空间复杂度: O(n)，其中 n 是队列中的元素个数。每个节点需要额外的空间存储两个指针。

完整代码实现

#include <iostream>
#include <stdexcept>
#include <vector>
using namespace std;

// 双向节点结构
struct DoubleNode {
    int value;           // 数据域
    DoubleNode* prev;    // 前驱指针
    DoubleNode* next;    // 后继指针

    DoubleNode(int val) : value(val), prev(nullptr), next(nullptr) {}
};

// 双端队列类
class Deque {
private:
    DoubleNode* front;   // 队首指针
    DoubleNode* rear;    // 队尾指针
    int size;            // 队列大小

public:

    Deque() : front(nullptr), rear(nullptr), size(0) {}

    ~Deque() {
        clear();
    }

 
    void enqueueFront(int value) {
        DoubleNode* newNode = new DoubleNode(value);

        if (isEmpty()) {
            front = newNode;
            rear = newNode;
        } else {
            newNode->next = front;
            front->prev = newNode;
            front = newNode;
        }

        size++;
    }


    void enqueueRear(int value) {
        DoubleNode* newNode = new DoubleNode(value);

        if (isEmpty()) {
            front = newNode;
            rear = newNode;
        } else {
            newNode->prev = rear;
            rear->next = newNode;
            rear = newNode;
        }

        size++;
    }

    int dequeueFront() {
        if (isEmpty()) {
            throw runtime_error("队列为空，无法从队首出队");
        }

        int value = front->value;
        DoubleNode* temp = front;
        front = front->next;

        if (front == nullptr) {
            rear = nullptr;
        } else {
            front->prev = nullptr;
        }

        delete temp;
        size--;
        return value;
    }

    int dequeueRear() {
        if (isEmpty()) {
            throw runtime_error("队列为空，无法从队尾出队");
        }

        int value = rear->value;
        DoubleNode* temp = rear;
        rear = rear->prev;

        if (rear == nullptr) {
            front = nullptr;
        } else {
            rear->next = nullptr;
        }

        delete temp;
        size--;
        return value;
    }

    int peekFront() {
        if (isEmpty()) {
            throw runtime_error("队列为空");
        }
        return front->value;
    }

    int peekRear() {
        if (isEmpty()) {
            throw runtime_error("队列为空");
        }
        return rear->value;
    }
        
    bool isEmpty() {
        return front == nullptr;
    }

    int getSize() {
        return size;
    }

    void clear() {
        while (!isEmpty()) {
            dequeueFront();
        }
    }

    vector<int> toArray() {
        vector<int> result;
        DoubleNode* current = front;

        while (current != nullptr) {
            result.push_back(current->value);
            current = current->next;
        }

        return result;
    }

    vector<int> toArrayReverse() {
        vector<int> result;
        DoubleNode* current = rear;

        while (current != nullptr) {
            result.push_back(current->value);
            current = current->prev;
        }

        return result;
    }

    void print() {
        if (isEmpty()) {
            cout << "队列为空" << endl;
            return;
        }

        cout << "队列内容（从前到后）: ";
        vector<int> arr = toArray();
        for (size_t i = 0; i < arr.size(); i++) {
            cout << arr[i];
            if (i < arr.size() - 1) {
                cout << " ↔ ";
            }
        }
        cout << endl;
        cout << "队首: " << peekFront()
             << ", 队尾: " << peekRear()
             << ", 大小: " << size << endl;
    }

    void printReverse() {
        if (isEmpty()) {
            cout << "队列为空" << endl;
            return;
        }

        cout << "队列内容（从后到前）: ";
        vector<int> arr = toArrayReverse();
        for (size_t i = 0; i < arr.size(); i++) {
            cout << arr[i];
            if (i < arr.size() - 1) {
                cout << " ↔ ";
            }
        }
        cout << endl;
    }
};

int main() {
    Deque deque;

    cout << " 测试队尾入队 " << endl;
    deque.enqueueRear(1);
    deque.enqueueRear(2);
    deque.enqueueRear(3);
    deque.print();
   

    cout << "\n 测试队首入队 " << endl;
    deque.enqueueFront(0);
    deque.enqueueFront(-1);
    deque.print();
  

    cout << "\n测试双向遍历 " << endl;
    deque.print();
    deque.printReverse();
   

    cout << "\n 测试队首出队 " << endl;
    cout << "队首出队: " << deque.dequeueFront() << endl;  // 输出: -1
    cout << "队首出队: " << deque.dequeueFront() << endl;  // 输出: 0
    deque.print();
   

    cout << "\n 测试队尾出队 " << endl;
    cout << "队尾出队: " << deque.dequeueRear() << endl;   // 输出: 3
    deque.print();
   

    cout << "\n 测试混合操作 " << endl;
    deque.enqueueFront(0);      // 队首添加 0
    deque.enqueueRear(3);       // 队尾添加 3
    deque.enqueueFront(-1);     // 队首添加 -1
    deque.enqueueRear(4);       // 队尾添加 4
    deque.print();

    cout << "\n 测试查看操作 " << endl;
    cout << "队首元素: " << deque.peekFront() << endl;  // 输出: -1
    cout << "队尾元素: " << deque.peekRear() << endl;   // 输出: 4
    cout << "队列大小: " << deque.getSize() << endl;    // 输出: 6

    cout << "\n 测试清空作 " << endl;
    deque.clear();
    cout << "清空后是否为空: " << (deque.isEmpty() ? "是" : "否") << endl;  // 输出: 是

    cout << "\n 测试边界情况：单元素操作 " << endl;
    deque.enqueueFront(100);
    deque.print();
    cout << "队首出队: " << deque.dequeueFront() << endl;
    cout << "队列是否为空: " << (deque.isEmpty() ? "是" : "否") << endl;

    return 0;
}

双端队列是非常重要的数据结构，我们在刷算法题的时候经常用到，但是大家不需要自己定义，直接用 STL 里的即可

优先队列（Priority Queue）

优先队列不按照先进先出的顺序，而是按照优先级出队，这块大家要结合堆排序来看

优先队列（最大堆）:
入队: 3, 1, 4, 1, 5, 9, 2, 6

内部结构（堆）:
       9
      / \
     6   5
    / \ / \
   1  1 4  2
  /
 3

出队顺序: 9, 6, 5, 4, 3, 2, 1, 1
（从大到小）

STL 优先队列

#include <iostream>
#include <queue>
using namespace std;

int main() {
    // 默认是最大堆
    priority_queue<int> maxHeap;

    maxHeap.push(3);
    maxHeap.push(1);
    maxHeap.push(4);
    maxHeap.push(1);
    maxHeap.push(5);

    while (!maxHeap.empty()) {
        cout << maxHeap.top() << " ";  // 5 4 3 1 1
        maxHeap.pop();
    }
    cout << endl;

    // 最小堆
    priority_queue<int, vector<int>, greater<int>> minHeap;

    minHeap.push(3);
    minHeap.push(1);
    minHeap.push(4);

    while (!minHeap.empty()) {
        cout << minHeap.top() << " ";  // 1 3 4
        minHeap.pop();
    }

    return 0;
}

下面简单总结一下队列的应用场景

队列的应用场景

**任务调度：**操作系统使用队列管理进程调度。
**广度优先搜索（BFS）：**BFS 使用队列遍历图或树。
**消息队列：**在分布式系统中，消息队列用于解耦生产者和消费者。
**缓冲区：**队列可以用作数据流的缓冲区。

04、队列

# 什么是队列

# 生活中的队列

# 队列的定义

# 队列 vs 栈

# 队列的基本操作

# 核心操作

# 队列的实现方式

# 基于数组的实现（循环队列）

# 基于链表的实现（重点）

# 核心操作实现

# 入队操作

# 出队操作

# 查看队首

# 判空

# 获取大小

# 时间复杂度分析

# 完整代码实现

# 与数组实现的对比

# 队列的变体

# 双端队列（Deque）

# 核心操作实现

# 队首入队

# 队尾入队

# 队首出队

# 队尾出队

# 查看队首和队尾

# 判空和获取大小

# 时间复杂度分析

# 完整代码实现

# 优先队列（Priority Queue）

# 队列的应用场景

什么是队列

生活中的队列

队列的定义

队列 vs 栈

队列的基本操作

核心操作

队列的实现方式

基于数组的实现（循环队列）

基于链表的实现（重点）

核心操作实现

入队操作

出队操作

查看队首

判空

获取大小

时间复杂度分析

完整代码实现

与数组实现的对比

队列的变体

双端队列（Deque）

核心操作实现

队首入队

队尾入队

队首出队

队尾出队

查看队首和队尾

判空和获取大小

时间复杂度分析

完整代码实现

优先队列（Priority Queue）

队列的应用场景